“En ota syyttävää otetta, vaan ammattimaisen ja ehkä jopa empaattisen: jos olisin itse ollut vastuussa Talvivaaran sääriskien ennakoinnista, kokisinko tällä hetkellä mokanneeni?…. [Lopputulos on, että] tämän tiedon pohjalta kokisin epäonnistuneeni. Vuoden 2012 sateet eivät olisi saaneet tulla yllätyksenä.”
Talvivaaran kaivosonnettomuus herättää tunteita, mutta toivon mukaan myös ajattelua ja harkintaa. Vaikka olenkin itse aktiivinen luonnonsuojeluliikkeessä ja niin ollen hyvinkin kriittinen kaivoksen toimintaa kohtaan, pyrin kuitenkin selvittämään asioita kylmän analyyttisesti. (Ks myös Talvivaara 2, jossa pyrin arvioimaan Talvivaaran esittämää tulevaisuuden riskinhallintaa).
En myöskään haukkaa liian isoa palaa, vaan otan tässä hyvin kapean osa-alueen: sääriskit. Talvivaara on pitänyt onnettomuuden eräänä syynä “historiallisen sateista” kesää ja syksyä, jonka takia vesiä on jouduttu varastoimaan erilaisin hätäratkaisuin. Talvivaaran mukaan näihin sateisiin ei olisi ollut mahdollista järkevästi varautua.
Onko näin?
Näen tässä kolme erillistä kysymystä:
1. Oliko vuosi 2012 todellakin “historiallisen sateinen” Kainuussa? (Koska murtuma tapahtui marraskuun alussa, riittää tutkia sateita lokakuun loppuun asti)
2. Vaikka olisikin, niin olisiko Talvivaaran silti pitänyt pystyä tilastollisesti ennakoimaan se?
3. Onko syytä olettaa, että vastaavanlaisia talvia voi tulla lisää?
En ota syyttävää otetta, vaan ammattimaisen ja ehkä jopa empaattisen: jos olisin itse ollut vastuussa Talvivaaran sääriskien ennakoinnista, kokisinko tällä hetkellä mokanneeni? En ota mitään kantaa siihen, mitä Talvivaara ehkä on tehnyt tai jättänyt tekemättä, vaan pyrin ainoastaan katsomaan, mitä säässä tapahtui. Jos jokin seikka mielestäni puolustaa Talvivaaran näkemystä, otan sen esille.
Tilastotieteessä mitään ei voi todistaa vääräksi tai oikeaksi. Voi korkeintaan esittää väitteitä, jotka ovat joko erittäin uskottavia tai sitten erittäin epäuskottavia. Näihin kysymyksiin ei siis ole kyllä-ei-vastauksia. Tässä osassa keskityn vain ja ainoastaan kysymykseen 1, ja siihenkin vasta osittain. Kirjoituksia tulee lisää, kunhan vain löydän aikaa niitä tehdä.
Olen tehnyt tätä analyysiä Suomen Luonto-lehdelle sen Ilmatieteen laitokselta hankkiman aineiston pohjalta. Tässä esitetty analyysi perustuu kyseiseen aineistoon ja voi toimia taustatietona lehden artikkeleihin, mutta on riippumatonta itse lehdestä. Ilmatieteen laitos ei ole vielä vapauttanut näitä datoja, joten en voi antaa raakadataa julkiseen käyttöön ilman laitoksen erillistä lupaa. Käytännössä toivon ja oletan, että Ilmatieteen laitos aikanaan tekee vastaavat analyysit tarkemmilla menetelmillä.
Suomen Luonto teki aiemmin Sotkamon sateisuusdatoista nopean analyysin (Suomen Luonnon blogi 19.11.2012). Sen perusteella ainakin vuonna 2004 tammi-syyskuu olisi ollut jopa sateisempi kuin tammi-syyyskuu 2012. Käytän tässä laajempaa ja pidempiaikaista datasettiä, ja hiukan perinpohjaisempia analyysimenetelmiä. Lopputulos on kuitenkin pitkälti sama: vuosi 2004 on ollut käytännössä yhtä paha sadevuosi, ja lähes yhtä pahoja on ollut viimeisten 50 vuoden aikana useita.
Mitä tarkoittaa “historiallinen”?
Termi ei ole yksikäsitteinen. Käytännössä se tarkoittaa, että sademäärä on suurempi kuin edelliseen V vuoteen. Mutta kuinka suuri on V? Riippuu asiayhteydestä.
Millä tahansa laitoksella on tietty laskettu elinkaari (Talvivaaralle vähintään 30 vuotta). Jokaisena vuonna on tietty todennäköisyys x, että sadetta tulee liikaa. Tätä x:ää voi yrittää arvioida historiallisen sadannan perusteella. Suomessa on sadedataa periaatteessa olemassa noin 150 vuoden ajalta, käytännössä kuitenkin huomattavasti lyhyemmältä.
Ensimmäisenä arviona: jos on käytössä S vuotta mittasarjaa, ja käytetään suurinta sadearvoa mitoittamaan kaivoksen toiminta, tulvimisriski on vähintään x=1/S. Toisin sanoen, jos sadan vuoden aikana suuri sademäärä on 1100 mm/vuosi, ja kaivos mitoitetaan kestämään alle tämä 1100 mm/vuosi sadanta, on 1/100 eli 1% todennäköisyys että jonain tiettynä vuotena se tulvii.
Lasku on suoraviivainen jos kaivos toimii useita vuosia. Todennäköisyys, että se pysyy kunnossa yhden vuoden, on (1-x), eli tässä tapauksessa 99%. Todennäköisyys, että se pysyy kunnossa N peräkkäistä vuotta, on (1-x)^N, ja vastaavasti tulvimisen todennäköisyys tänä aikana on p=1-(1-x)^N.
Alla on laskettu yleisellä tasolla, mikä on tulvimistodennäköisyys eri arvoille N (pystyrivi) ja S (vaakarivi). Punaisella on merkitty tapaukset, joissa todennäköisyys on 50% tai yli — ts on todennäköisempää että kaivos tulvii elinaikanaan, kuin että se toimisi häiriöttä. Tällaista tilannetta tuskin kukaan suostuu hyväksymään. Keltaisella on tapaukset, joissa todennäköisyys on 25%. Tämäkin on suurehko luku, jos ajatellaan että kaivoksia olisi Suomessa useita.
Luvut eivät suoraan kerro itse Talvivaaran tapauksesta mitään. Ne kuitenkin osoittavat, että pohjana käytettävän aikasarjan on oltava yllättävän pitkä. Kaivosten tapauksessa on kyseenalaista, riittääkö edes 150 vuotta. Mitoituksiin laitetaan totta kai erilaisia varmuuskertoimia päälle; mutta jos alkuperäinen luku ei ole oikein, ei varmuuskerroin tilannetta välttämättä pelasta.
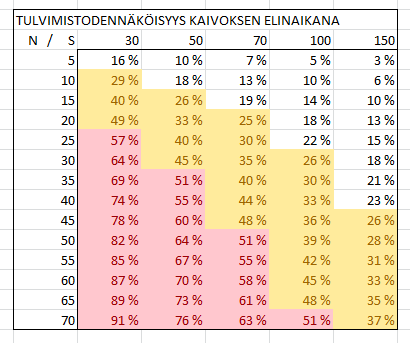
Kuva 1: Tulvimisen todennäköisyys, kun laitos toimii N vuotta ja sen toiminta mitoitetaan edellisten S:n vuoden suurimman sadannan mukaan.
Miten sadantaa pitäisi mitata?
Pitkän ajan sadetilastot annetaan yleensä kalenterivuoden kertyminä. Tämä voi antaa pahastikin harhaanjohtavia tuloksia.
Oletetaan, että tammi-kesäkuussa ei sada ollenkaan. Heinäkuussa alkaa sataa 100 mm/kuukausi, ja sataa samaa tahtia seuraavaan heinäkuuhun, minkä jälkeen sade loppuu. Vuoden aikana on tullut vettä 1200 mm, mikä on reilusti Suomen ennätys ja ehkä vuosisadan tulva. Kalenterivuosien mukaan kuitenkin molempina vuosina on satanut 600 cm. Vuositilasto näyttää kaksi peräkkäistä normaalia vuotta.
Siksi onkin parempi käyttää liukuvaa vuosisadantaa. Joka kuussa lasketaan yhteen edellisten 12 kuukauden sademäärä. Tämä antaa ennen muuta luotettavan kuvan maksimisadannasta.
Käytännön ongelmissa voi myös jokin muu aikaväli olla järkevä. Jos esimerkiksi lantaa säilötään avosäiliössä ja levitetään aina keväällä ja syksyllä, lantasäiliöiden ylitulvimisen kannalta vain kuuden kuukauden sadannalla on merkitystä. Sen jälkeen säiliö tyhjennetään, ja laskenta voi alkaa alusta. (Käytännössä asia ei tietenkään ole aivan näin yksinkertainen).
Talvivaaran tapauksessa sadevettä on vastaavasti laskettu poistuvan esimerkiksi haihdunnan ja erilaisten prosessivaiheiden kautta. Koska näistä ei ole tarkempaa tietoa, en pysty arvioimaan, mikä olisi oikea aikaväli. On kuitenkin hyvä lähtökohta, että vuoden aikana satanut vesi täytyy saada hoidettua pois saman vuoden aikana.
Käytetty data
Käytetyt viisi sadeasemaa on piirretty kuvaan 2. Kuolaniemi on aloittanut toimintansa vasta 2010, muut aiemmin(Kaarakkala ja Paltaniemi 1959, Saviho 1967, Saaresmäki 1970). Alueella on myös ollut joitakin jo suljettuja sadeasemia, joden datoja en ole vielä saanut, kuten en myöskään datoja ennen vuotta 1959. Otan ne myöhempiin analyyseihin mukaan.
Mikään asemista ei vastaa suoraan Talvivaaraa. Paikallinen sade voi vaihdella rajusti, erityisesti kun korkeuserot ovat suuria. Saviaho on selvästi lähin (n 20 km) ja Sääresmäki kaukaisin (yli 60 km); toisaalta Saviahon korkeus on vain 150 metriä, kun taas Talvivaara on yli 200 metrin korkeudessa. Lisäksi Saviaho on Talvivaaran selänteen itäpuolella, ja saattaa jäädä vaarojen katveeseen.
Näin ollen on lähdettävä siitä, että mikään asemista ei kuvaa Talvivaaraa täydellisesti. Yhden ainoan luvun sijasta on katsottava kaikkien asemien sademääriä ja asemien välistä hajontaa. Käytän asemien keskimääräistä sadantaa tilanteen havainnollistamiseen, mutta se ei välttämättä ole “oikea” arvo. Toisaalta asemien maksimisadantoja voi suoraan käyttää pahimpien tilanteiden arviointiin: jos jollakin asemalla on satanut yli 900 mm, se tarkoittaa että jossain päin Kainuuta voi sataa yli 900 mm, ja kaivos on mitoitettava sen mukaisesti.

Kuva 2: Sadeasemat. Lähde: http://kansalaisen.karttapaikka.fi
Pitkän skaalan seuranta: 1961-2012
Vuoden 1961 jälkeiset vuotuiset liukuvat sateisuusarvot on piirretty kuvaan 2. Eri asemien sademäärät vaihtelevat, mutta korreloivat kuitenkin merkitsevästi (vähintään arvolla r=0.75). Keskiarvo kuvastaa jollakin tasolla “koko Kainuun” sadantaa, mutta eri asemien välillä voi olla lähes 200 cm heittoa.
Kuvan perusteella Kainuussa on ollut useitakin vuoden 2012 tyyppisiä sadevuosia. Varsinkin talvet 2007/8 ja 2004/5 ovat olleet ongelmallisia, samoin kuin 1992 ja 1988/9. Näissä kaikissa sadanta on ollut yli 900 mm/vuosi. Yli 800 mm/vuosi sadantaa on esiintynyt lisäksi kuusi kertaa, 2000/1, 1983, 1982, 1974, 1968, ja 1962.
Ainakin Saaresmäessä on selkeästi rikottu tämän mittausvälin sade-ennätys. Toisaalta Talvivaaraa läheisemmillä asemilla ei olla sen suuremmissa luvuissa kuin aiempinakaan hankalina vuosina.

Kuva 3: 12 kk sadanta, vuodet 1961-2012
Tarkempi tarkastelu: 1989-2012
Otetaan tarkemmaksi tarkasteluväliksi 1998-2012. Kuvassa 3 on tämän aikavälin kuukausittaiset sademäärät. Syksyn 2012 sateet ovat kovia, mutta suurempiakin yksittäisiä sademääriä on ollut mm 2007 ja 2004. Syksyllä 2012 nämä kovat sateet ovat kuitenkin jatkuneet monta kuukautta, mikä varmasti aiheuttaa ongelmia.
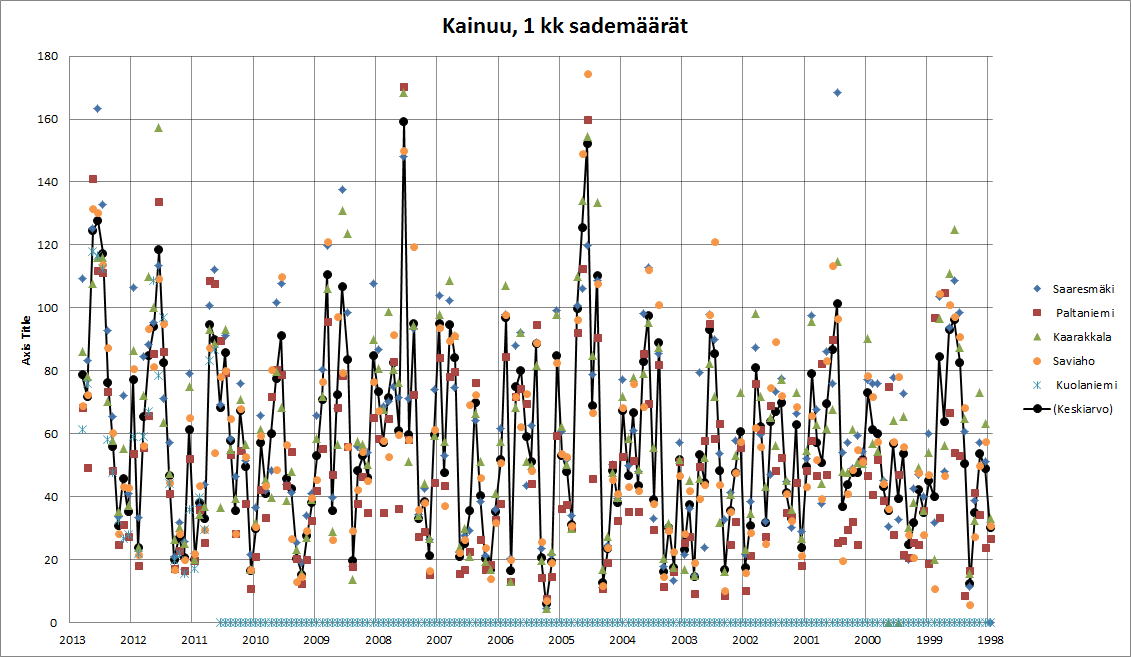
Kuva 4: Kuukausittainen sademäärä, vuodet 1989-2012
Jatkuvien sateiden merkityksen näkee parhaiten piirtämällä pidempien aikojen liukuvaa sadantaa. Kuvassa 4 on kolmen kuukauden sadannat. Tämän perusteella syksy 2012 olisi jokseenkin samantyyppinen kuin 2004. Pahin tilanne olisi tämän mukaan alkanut lokakuussa olla jo ohi.

Kuva 5: 3 kk sadanta, vuodet 1989-2012
Kuuden kuukauden sadanta (kuva 6) kuitenkin osoittaa, että tilanne on veden kertymisen kannalta aidosti hankala. Silti tälläkin mittarilla vuosi 2012 on samaa luokkaa kuin vuosi 2004. Koska vuosi 2012 jatkuu yhä, on täysin mahdollista että vuoden 2004 lukemat tullaan ylittämään. Tämä ei kuitenkaan ollut tilanne vielä kipsisakka-altaan vuodon hetkellä.

Kuva 6: 6 kk sadanta, vuodet 1989-2012
Kuva 7 on kuvan 2 zoomaus. Tämänkään perusteella on vaikea perustella, että vuosi 2012 eroaisi vuodesta 2004. Saaresmäen lukema toki liikkuu omalla tuhatluvullaan, mutta muiden asemien lukemat eivät ole poikkeuksellisia. Mikä on “totuus”? Sitä ei tästä datasta pysty päättelemään.

Kuva 7: 12 kk sadanta, vuodet 1989-2012
Mitä tästä opimme?
Kuten tilastotieteessä valitettavan usein, emme oppineet mitään ehdottoman varmaa. Tärkeä opetus on joka tapauksessa se, että ei riitä katsella kalenterivuoden mukaan tehtyjä tilastoja, vaan vuosisadantaa on seurattava kuukausittain. Tämä saattaa muuttaa johtopäätöksiä merkittävästikin.
On selvää, että vuosi 2012 on ollut sateisuuuden kannalta Kainuussa vaikea, ennen muuta siksi, että sekä kesä että syksy ovat olleet sateisia. Viimeisten 50 vuoden aikana on kuitenkin ollut vähintään kaksi muuta vuotta, jotka näyttävät lähes yhtä pahoilta (2007 ja ennen muuta 2004). Yli 800 mm vuosisadantaa on sen lisäksi ollut kahdeksana vuonna. Kalenterivuosien mukaan kerätyissä tilastoissa nämä katoavat.
Tilannetta toki hankaloittaa se, että pahimmat sadejaksot ovat tapahtuneet vasta 2000-luvulla, kun kaivoksen suunnittelu on jo ollut hyvän aikaa käynnissä. Poikkeuksellisia sateita on kuitenkin ollut myös 1960-2000. Tämä mittausaika (50 vuotta) on käytännössä aivan liian lyhyt, kun pyritään arvioimaan riskejä näin pitkäikaiselle kaivokselle. Pyrin etsimään vielä käsiini vanhempaa aikasarjaa, sekä datat myös niistä alueen sadeasemista, jotka on jo suljettu. Vasta silloin voin kunnolla vastata kysymykseen 1.
Vuosi 2012 (lokakuun loppuun asti) on siis sadannaltaan ollut todella vaikea. Ainutlaatuiselta se ei kuitenkaan vaikuta. Vanhojen datojen tarkka analyysi osoittaa, että Kainuussa on esiintynyt lähes tämänkaltaisia sadekertymiä jo useasti vuoden 1960 jälkeen, ja ennen muuta vuonna 2004 on ollut pitkälti vastaava vuosi. Jos itse olisin vastuussa sääriskien ennakoinnista, tämän tiedon pohjalta kokisin epäonnistuneeni. Vuoden 2012 sateet eivät olisi saaneet tulla yllätyksenä.
Kirjoituksen kakkososassa yritän arvioida, onko Talvivaaran riskinhallintasuunnitelma jatkoa ajatellen riittävä.
Kiitokset: Kiitän Ilmatieteen laitosta sateisuusdatasta. Analyysiin ovat tuoneet merkittävää lisäarvoa mm Antti Halkka (Suomen Luonto-lehti), Pertti Sundqvist, Helvi Heinonen-Tanski, ja Heikki Simola.
Muita kirjoituksia: Avoin seuranta , Talvivaara. Yleisiä ympäristökirjoituksia: Ympäristö.
Like this:
Like Loading...


